Stress and Strain: Definition, Formula,Types in detail, [Notes & PDF]

Table of Contents

Stress and strain are two quantities that are used to define the nature of the applied force and resulting deformation.

In this article, we will be studying Definition, Formula, Types, Curve Diagram, and Differences in stress and strain.

You can download whole document in PDF format from just below the articles.

So let’s start with the stress definition,

Stress Definition:

Stress is defined as the internal restoring force applying per unit area of the deformed body.

Stress developed in a body depends upon how much external force acted on it.

Stress Formula:

It is measured as the external force applying per unit area of the body i.e,

Stress = External deforming force (F)/Area (A)
Its SI unit is Nm^-2 or N/m².
Its dimensional formula is [ML^-1T^-2].

E.g., If the applied force is 10N and the area of cross section of the wire is 0.1m², then stress = F/A = 10/0.1 = 100N/m².

Types of Stress:

There are mainly 3 types of stresses:

Tensile stress
Compressive stress
Tangential stress

Tensile stress: Tensile stress is defined as the increase in length of the body due to applied force.

Compressive stress: It is defined as the decrease in length of the body due to applied force.

Tangential stress: It is defined as the deforming force applied per unit area.

Strain Definition:

Strain is defined as the change in shape or size of a body due to deforming force applied on it.

We can say that a body is strained due to stress.

Strain Formula:

Its symbol is (∈).

Strain is measured by the ratio of change in dimension to the original dimension. i.e,

Strain (∈) = Change in dimension / Original dimension

Since it is ratio of two similar quantities, it is a pure number.

Therefore, Strain has no SI unit. It is dimensionless.

Types of strain:

Strain also have 3 types:

Longitudinal strain
Volumetric strain
Shearing strain

Longitudinal strain: When the deforming force makes change in length alone, the strain produced is called longitudinal strain.

It is measured as the ratio of change in length to its original length.

Volumetric strain: When the deforming force makes change in volume, the strain is called volumetric strain.

It is measured by the ratio of change in volume to the original volume.

Shearing strain: When the deforming force makes change in shape of the body, the strain is called shearing strain.

It is measured as the ratio of the displacement of the surface that is in direct contact with the applied shear stress from its original position.

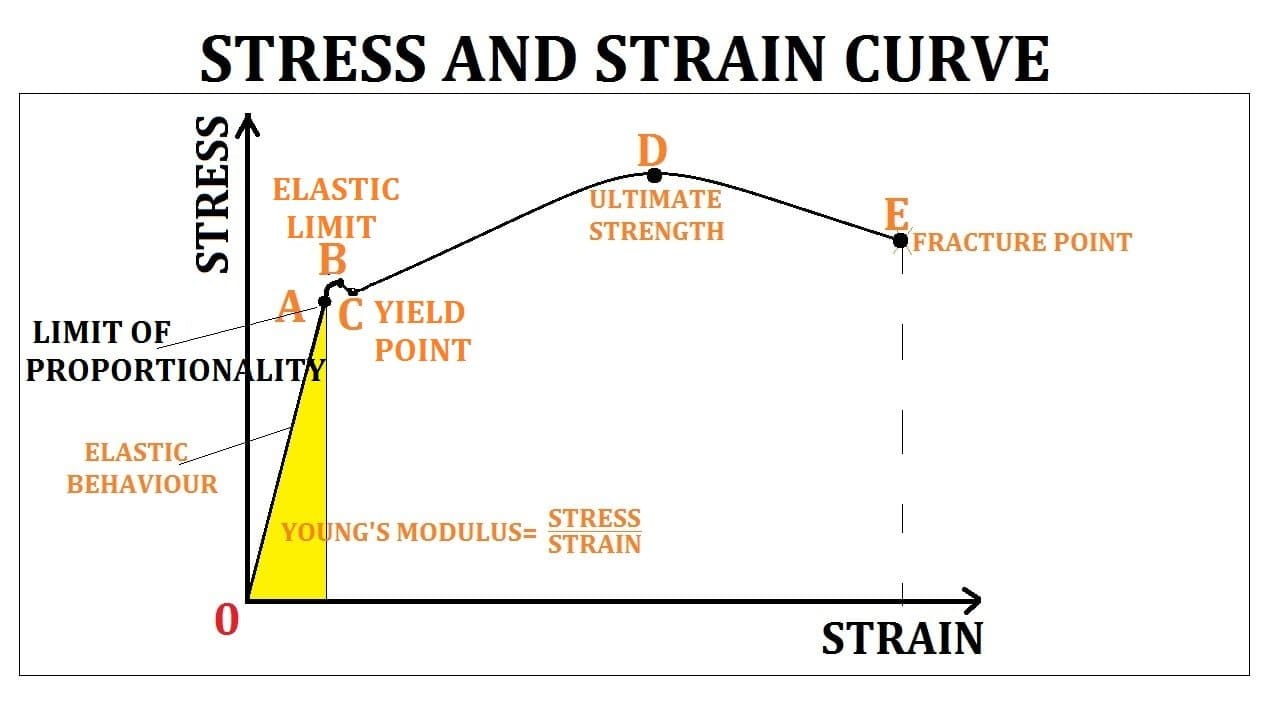
Stress and Strain Curve for an Elastic Material:

Suppose a wire of uniform cross-section is suspended from a rigid support. When the load at other side is increased gradually, then length of wire goes on increasing.

If we plot the graph between stress and strain, then shape of the curve will be as shown in fig just below:

Let us describe all the points of the graph:

Portion O-A (Elastic Behavior):

The portion OA of the graph is a straight line showing that up to point A, Stress produced in the wire is directly proportional to the strain i.e., stress ∝ strain.

In this portion Hooke’s law is being obeyed by the material of the wire. The point A is termed as Limit of Proportionality.

The proportionality of limit is the maximum stress that a material can hold without the departure from a linear stress-strain relation. If the applied force from any point between O and A is removed, then wire will regains its original length.

Portion A-B:

In Portion AB of the graph, stress is not directly proportional to the strain of the material.

Note that slope of graph is decreased; this means that strain increases more rapidly with strain. The point B is termed as Elastic limit.

Elastic limit of a body is maximum stress which a body can sustain and still regain its original shape and size if load is removed.

Portion B-C:

If the load is increased beyond elastic limit, a point C is reached at which there is marked increase in extension. The point C is termed as Yield Point.

Between B and C, material becomes plastic i.e., if applied force is removed from any point between B and C, material will not regain its original shape and size.

The extension not recoverable after the removal of applied force is called as permanent set. Here OO’ is the permanent set.

Portion C-D:

If stress is increased beyond C, the wire lengthens rapidly until we reach at point D at the top of the curve. The point D is termed as Ultimate strength or Breaking stress.